
Jednym z podstawowych kryteriów doboru sprzętu pomiarowego do mierzonej charakterystyki jest stosowanie zasady „1 do 10”. Stwierdza ona, że rozdzielczość efektywna urządzenia pomiarowego powinna być co najmniej o rząd większa (czyli 10 razy) od szerokości przedziału tolerancji lub szerokości przedziału zmienności.
Dociekliwy inżynier może zadać sobie pytanie, skąd to wymaganie oraz co oznacza słowo „lub” i którą z tych wartości wybrać? Odpowiedź staje się dosyć prosta, gdy wcześniej wyjaśnimy sobie, co jest celem całego procesu pomiarowego i w jaki sposób uzyskane dane pomiarowe wpływają na ocenę statystyczną procesu. Jak wiadomo, analiza systemów pomiarowych (MSA) jest narzędziem ściśle związanym z innym, czyli ze statystycznym sterowaniem procesami (SPC). Głównym celem analizy MSA jest badanie zmienności systemu pomiarowego w celu oceny wpływu tegoż systemu na uzyskiwane pomiary charakterystyk wyrobu lub procesu.
Histogram a obraz procesu
Z drugiej strony musimy pamiętać, że jednym z kryteriów oceny zdolności procesu jest analiza rozkładu tego procesu. Tu z kolei podstawowym narzędziem jest histogram, który przybliża nam rzeczywistą krzywą rozkładu poprzez utworzenie wykresu słupkowego. Tak powstały histogram pozwala nam następnie wnioskować, czy w naszym procesie nie występują przyczyny specjalne, oraz czy mamy do czynienia z rozkładem normalnym bądź innym. Z kolei ta ostatnia obserwacja wpływa na przyjęty model obliczeniowy podczas wyznaczania współczynników zdolności.
Wyobraźmy sobie teraz, że dysponujemy urządzeniem pomiarowym o efektywnej rozdzielczości 0,05mm (np. suwmiarka), którym mierzymy jakąś charakterystykę wyrobu o szerokości przedziału tolerancji 0,6mm. Oznacza to, że jeżeli wszystkie produkowane wyroby mieszczą się w tolerancji, wówczas suwmiarka będzie w stanie rozróżnić co najwyżej 11 różnych wartości. Oznacza to jednocześnie, że chcąc sporządzić histogram z uzyskanych wartości, będzie on mógł mieć co najwyżej 11 klas (co odpowiada 11 słupkom na wykresie).
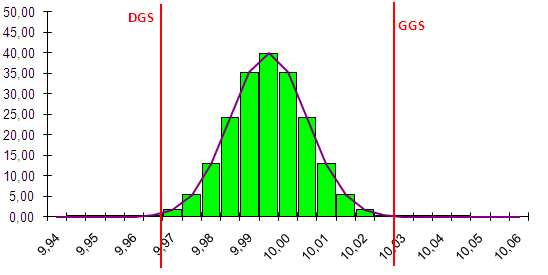
Praktyka statystyczna potwierdza, że taka liczba klas jest wystarczająca do oceny rozkładu procesu i wnioskowania o rodzaju rozkładu. A więc wydaje się, że takie postępowanie pomiarowe jest prawidłowe. Niestety w realnym życiu bardzo często zapomina się, że szerokość przedziału zmienności procesu nie zawsze jest tożsama z tolerancją. Warto tu przypomnieć, że w przemyśle motoryzacyjnym (i nie tylko) za szerokość tego przedziału przyjmuje się zwykle 6 odchyleń standardowych (6 sigma), czyli przedział, w którym powinno się znaleźć około 99,73% wartości z całej populacji. Wartość 6 sigma służy między innymi do wyznaczania współczynnika zdolności Cp lub Pp, wyrażanego wzorem:
$$Cp, Pp = \frac{{USL} – LSL}{6 \cdot s}\tag{1}$$
gdzie
USL – górna granica specyfikacji (upper specification limit)
LSL – dolna granica specyfikacji (lower specification limit)
Jakie wnioski wynikają z tego wzoru? Jeżeli wartość współczynnika Cp jest zbliżona do 1, wówczas w przedziale tolerancji (USL-LSL) znajduje się ok. 99,73% uzyskanych wyników pomiarów badanej charakterystyki. W takim przypadku przyjęcie założenia, że zasada „1 do 10” odnosi się do szerokości przedziału tolerancji jest słuszne, bo mamy szansę „zapełnić” wszystkie klasy tworzonego histogramu.
Rozdzielczość pomiaru a zdolny proces
Co jednak w sytuacji, gdy współczynnik zdolności procesu wynosi na przykład 2 lub więcej? Idąc wspomnianym tokiem rozumowania dochodzimy do wniosku, że szerokość przedziału zmienności (6 sigma) jest wówczas 2 razy węższa niż szerokość tolerancji, a więc dotychczasowe 99,73% wszystkich wartości znajdzie się nie w całym przedziale tolerancji, a w połowie tego przedziału. Jak praktycznie przełoży się na tworzony histogram? Jeżeli zasadę „1 do 10” przyjęto w odniesieniu do szerokości przedziału tolerancji, może się wówczas okazać, że uzyskane wyniki pokryją tylko 5, 6 klas (pojawi się tylko 5 lub 6 słupków na histogramie), co może znacznie utrudnić nasze wnioskowanie o rodzaju rozkładu z jakim mamy do czynienia. W przedstawionym przykładzie prawidłowym byłoby więc zastosowanie urządzenia pomiarowego o rozdzielczości efektywnej co najmniej dwa razy większej, czyli np. suwmiarki o rozdzielczości 0,02mm.
W skrajnym przypadku może dojść do sytuacji, że rozrzut procesu jest na tyle mały w stosunku do rozdzielczości urządzenia pomiarowego, że uzyskujemy tylko jedną i wciąż tą samą wartość pomiarową. Wówczas nasze urządzenie, z założenia przeznaczone do mierzenia cechy ciągłych, zostaje zdegradowane do rangi sprawdzianu a o jakimkolwiek wnioskowaniu co do rozkładu rozrzutu nie może być mowy.
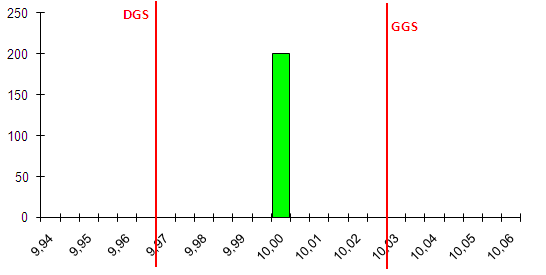
Przypomnijmy więc jeszcze raz zasadę „1 do 10”, lecz poddaną lekkiej modyfikacji: rozdzielczość urządzenia pomiarowego powinna być o rząd większa od mniejszej z dwóch wartości: szerokości przedziału tolerancji lub szerokości przedziału zmienności (rozumianego jako 6 odchyleń standardowych). Dopiero takie podejście pozwoli nam uzyskać wyniki umożliwiające właściwe klasowanie, a tym samym interpretowanie uzyskiwanych histogramów.
Zobacz też:
Interpretacja współczynnika %GRR w odniesieniu do zmienności pomiaru i przedziału tolerancji





