Jednym z celów badań MSA jest wyznaczenie współczynnika %GR&R i porównanie go z kryteriami akceptacji, definiowanymi przez podręcznik AIAG MSA lub wymagania klientów. Pojawia się jednak pytanie, w odniesieniu do czego należy wyznaczać ten współczynnik? Okazuje się, że odpowiedź nie jest jednoznaczna.
Możliwe jest kilka wariantów, których zastosowanie zależy od klienta, dla którego przeprowadzamy analizę, jak i od innych czynników.
WARIANT 1: Współczynnik %GR&R jako procent zmienności procesu wyznaczonej na podstawie próbek wziętych do badania
Zanim rozpoczniemy wyjaśnianie, czym jest współczynnik %GR&R liczony w odniesieniu do zmienności procesu (dla wygody oznaczymy go skrótem %GR&RTV), warto zwrócić uwagę, że na pewnym etapie analizy powtarzalności i odtwarzalności jest wyznaczany bezwzględny współczynnik GR&R (bez poprzedzającego procentu), z którego następnie jest obliczana wartość procentowa %GR&R. Bezwzględny współczynnik GR&R jest odchyleniem standardowym zmienności pomiaru, które wyznaczono w trakcie badania.
Aby to odchylenie standardowe nabrało praktycznego znaczenia, należy je porównać z pewną wartością odniesienia. W omawianym wariancie tą wartością jest zaobserwowana zmienność procesu TV (total variation) 1.
Skąd pochodzi wartość TV? W „klasycznym” podejściu, opisanym w podręczniku AIAG MSA, TV jest wyznaczane na podstawie zmienności próbek wziętych do badania 2. Dla przypomnienia dodajmy, że do badania GR&R standardowo wybiera się 10 sztuk (próbek) możliwie najlepiej reprezentujących zmienność procesu. Na marginesie warto tu dodać, że im bardziej zróżnicowana próbka (większe różnice między wartościami badanej charakterystyki), tym większa szansa, że w badaniu uzyska się pozytywny wynik – a więc niską wartość współczynnika %GR&RTV.
Załóżmy, że rozpatrujemy pewien system pomiarowy, który będzie oceniał wartość charakterystyki geometrycznej (np. długość), dla której dolna i górna granica specyfikacji wynoszą odpowiednio: LSL=20,00mm USL=22,00mm. Na poniższym rysunku zostały one oznaczone kolorem zielonym.
W procesie zmierzono 25 wyrobów, a kolejno odczytane wartości naniesiono na wykres w postaci niebieskiej łamanej linii. Z pomiarów tych wyznaczono również odchylenie standardowe (próbka powinna być większa, jednak dla czytelności przykładu pokazano tylko 25 pomiarów), a następnie niebieskimi poziomymi liniami wyznaczono obszar sześciu odchyleń standardowych (6 * sigma), który będziemy tu nazywać obserwowaną zmiennością procesu/próbek, czyli TV. Z kolei czerwona linia symbolizuje zmienność samego pomiaru, powodowaną takimi czynnikami jak brak powtarzalności i odtwarzalności (ang. repeatability and reproducibility). W uproszczeniu można powiedzieć, że linia ta symbolizuje zmienności występujące przy pomiarach kolejnych sztuk. Czerwone poziome linie wyznaczają 6 * sigma tego błędu.
Na rysunku 1 widać, że zmienność pomiaru GR&R (czerwona linia) jest wielokrotnie mniejsza niż obserwowana zmienność badanych próbek TV (niebieska linia).
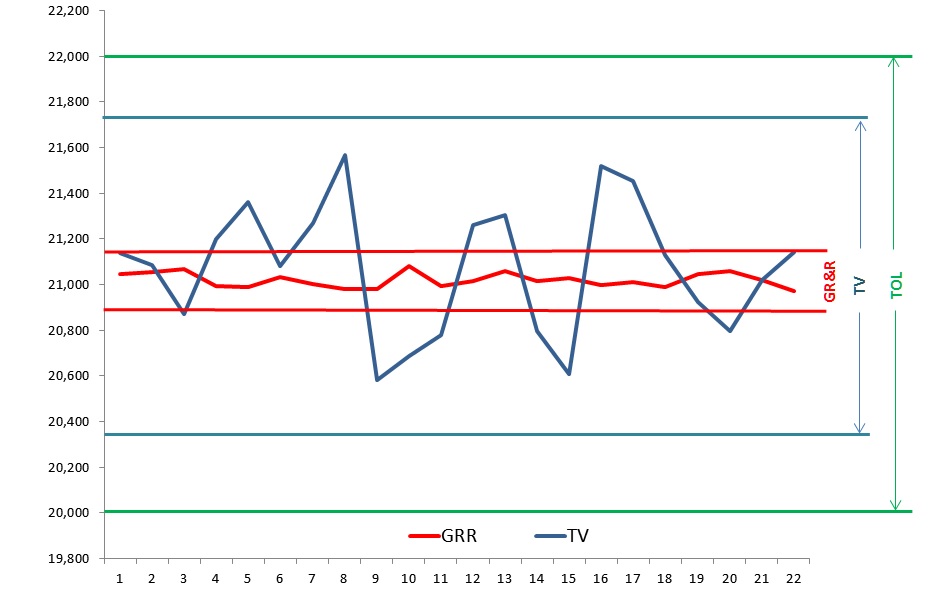
Jak już powiedzieliśmy, współczynnik %GR&R w omawianym wariancie informuje o stosunku zmienności pomiaru (na rysunku 1 szerokość przedziału wyznaczonego czerwonymi poziomymi liniami) do obserwowanej zmienności próbek (szerokość przedziału wyznaczonego niebieskimi poziomymi liniami). W przedstawionym przykładzie można oszacować, że uzyskany w ten sposób współczynnik %GR&R wynosi około 20%.
Załóżmy teraz, że taki sam system pomiarowy (a więc cechujący się podobną zmiennością pomiaru) jest używany do oceny procesu produkcyjnego o znacznie niższej zmienności (zakładając, że przedział tolerancji jest taki sam, proces ten będzie miał znacznie większą zdolność niż przedstawiony na rysunku 1). Sytuację obrazuje poniższy wykres:
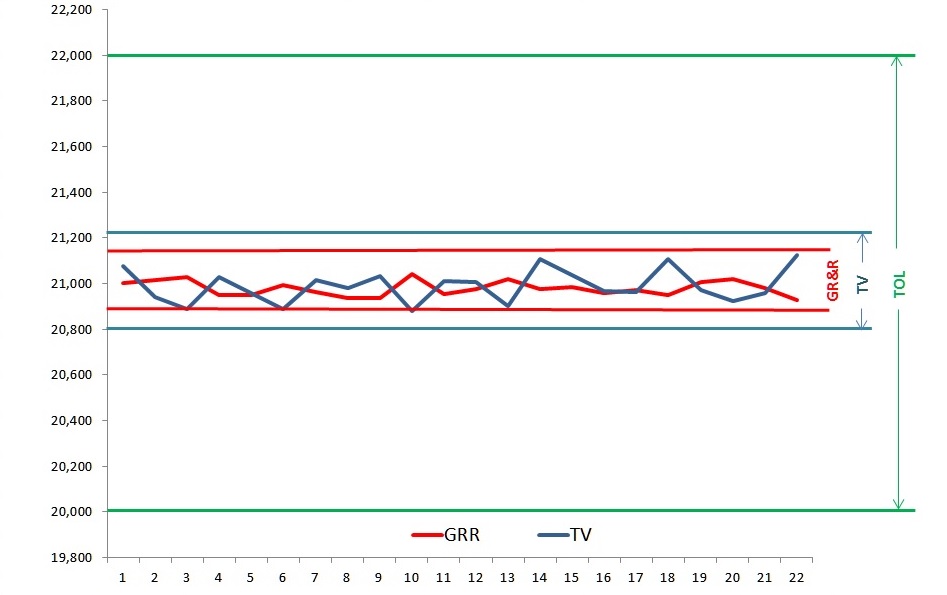
Jak widać, przy takiej samej zmienności pomiaru współczynnik %GR&RTV wyniesie około 70%, ponieważ taki jest stosunek zmienności pomiaru (GR&R) do obserwowanej zmienności procesu (TV).
Wyłania się z tego ciekawy wniosek – im zdolniejszy proces produkcyjny, w którym używamy określonego systemu pomiarowego, tym trudniej będzie uzyskać satysfakcjonującą wartość współczynnika %GR&RTV.
Kolejny wniosek jest taki, że wraz z doskonaleniem procesu produkcyjnego, a więc zmniejszaniem się zmienności tego procesu, należałoby równolegle doskonalić system pomiarowy, który ten proces ocenia. Wszystko po to, aby system pomiarowy ciągle wykazywał wystarczającą rozróżnialność konieczną do oceny zmienności danego procesu.
Takie rozumowanie prowadzi jednak do działań, które często okazują się ekonomicznie nieuzasadnione – doskonalenie systemu pomiarowego może na przykład oznaczać konieczność zwiększenia rozdzielczości pomiaru poprzez zastosowanie droższych urządzeń pomiarowych. W skrajnym przypadku, gdy proces jest bardzo zdolny a mierzona charakterystyka ma stosunkowo wąski przedział tolerancji, może się okazać, że brak technologii pomiarowych zapewniających wymaganą rozdzielczość pomiaru albo są one bardzo kosztowne. Jednocześnie warto zauważyć, że sytuacja przedstawiona na rysunku 2 obrazuje proces bardzo zdolny, a więc o małym ryzyku wygenerowania wyrobu niezgodnego.
W takim przypadku należy wrócić do podstawowego pytania: Co jest celem pomiaru? Po co wykonujemy pomiar? Nawiązując do wcześniejszych rozważań możemy sformułować następującą tezę: dążymy do wystarczająco rozdzielczego poznania zmienności procesu produkcyjnego. Dążenie to wynika głównie z potrzeby jak najlepszego poznania rozkładu procesu, co z kolei jest niezbędne do poprawnego wyznaczenia współczynników zdolności procesu (np. Cp/Cpk lub Pp/Ppk). Jednak nie należy zapominać, że ocena zdolności procesu jest przeprowadzana przede wszystkim w celu oszacowania ryzyka wyprodukowania wyrobu niezgodnego. A przecież powiedzieliśmy już, że sytuacja przedstawiona na rysunku 2 odpowiada procesowi bardzo zdolnemu, w którym to ryzyko jest niewielkie. Prowadzi to do następującego wniosku: im zdolniejszy proces (im mniejsza obserwowana zmienność procesu), tym mniejszą wagę można przykładać do prawidłowego rozpoznania jego rozkładu, a więc tym mniejsze znaczenie ma zdolność systemu pomiarowego do rozpoznawania tej zmienności.
Miarą tej zdolności jest tzw. efektywna rozdzielczość systemu pomiarowego, wyrażana za pomocą współczynnika ndc, nazywanego też liczbą rozróżnialnych kategorii pomiarowych (ang. number of distinct categories). Można więc sformułować końcowy wniosek: w przypadku systemu pomiarowego używanego do oceny wysoce zdolnego procesu nie jest konieczne uzyskanie wymaganego poziomu ndc (minimum 5, zgodnie z podręcznikiem AIAG MSA).
Niestety taka interpretacja nie jest jednoznacznie sformułowana w podręczniku MSA. Zaczynają ją jednak dostrzegać niektórzy klienci. Na przykład można ją znaleźć w podręczniku Ford Motor Company Customer-Specific Requirements For use with PPAP 4.0. W części dotyczącej analiz MSA (rozdział 8) zamieszczono następującą uwagę:
Note: in the special case where the manufacturing process is very capable, stable and in control (e.g. Ppk > 2.5), percent tolerance is used, the number of distinct categories is not applicable (…).
Co przetłumaczymy następująco: „W specjalnych przypadkach, gdy proces produkcyjny jest bardzo zdolny, stabilny i sterowalny (np. Ppk > 2,5), [współczynnik %GR&R – P.S.] można wyznaczyć jako procent tolerancji a liczba rozróżnialnych kategorii (ndc) nie ma zastosowania (…).”
Zwróćmy uwagę, że w zdaniu tym pojawia się jeszcze propozycja wyznaczenia współczynnika %GR&R jako procentu tolerancji. Tę kwestię wyjaśniono poniżej.
WARIANT 2: Współczynnik %GR&R jako procent tolerancji
Okazuje się, że współczynnik %GR&R można wyznaczyć jeszcze inaczej. Zamiast dzielić uzyskane odchylenie standardowe GR&R przez zaobserwowaną zmienność procesu produkcyjnego (TV), w mianowniku możemy użyć szerokości przedziału tolerancji (TOL). Wartość tego współczynnika będzie informowała nas, jaki jest stosunek zmienności pomiaru do przedziału tolerancji, a nie jak poprzednio – do obserwowanej zmienności procesu. Współczynnik ten w dalszej części artykułu będziemy oznaczać skrótem %GR&RTOL.
Wartość współczynnika %GR&RTOL jest szczególnie przydatna, gdy chcemy ocenić przydatność systemu pomiarowego używanego do sortowania wyrobów. Dotyczy to więc przede wszystkim procesów o niskiej zdolności, w których pojawia się znaczna liczba niezgodności. Zwróćmy uwagę, że w takim przypadku podstawowym problemem nie jest już to, czy poprawnie oceniamy zdolność procesu produkcyjnego, ale czy poprawnie oceniamy zgodność lub brak zgodności wyrobu. Obrazuje to poniższy rysunek:
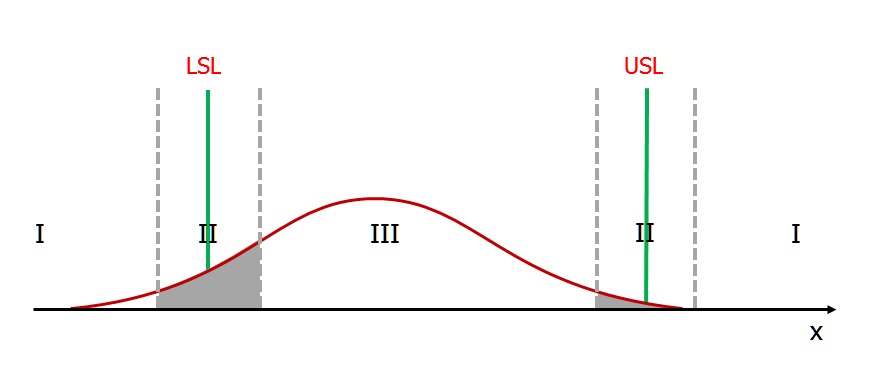
Zakładające, że na powyższym rysunku fragment krzywej rozkładu odpowiada 6*sigma procesu (albo ogólniej: obejmuje 99,73% wszystkich wyników), możemy łatwo wykazać, że mamy do czynienia ze słabo zdolnym procesem, o zdolności poniżej 1 (ponieważ 6*sigma > TOL to automatycznie Cp < 1, ponieważ Cp = TOL / (6*sigma)).
Jak widać na rysunku, w takim przypadku znaczna część pomiarów jest uzyskiwana w pobliżu granic specyfikacji. Niestety, ze względu na występującą zmienność pomiaru, niektóre wyniki są obarczone dużą niepewnością (szare strefy przy granicach specyfikacji, oznaczone cyfrą II). W tych strefach pojawia się ryzyko błędnej kwalifikacji wyrobu, co generuje dwa koszty złej jakości: przyjęcie wyrobu niezgodnego jako zgodnego wiąże się z ryzykiem reklamacji, a sytuacja odwrotna, czyli odrzucenie wyrobu zgodnego (tzw. false alarms), powoduje niepotrzebne straty. W szczególności jednak jesteśmy zainteresowani zabezpieczeniem interesów klienta, a więc uniknięciem pierwszego błędu (tzw. type one error), czyli uznania wyrobu niezgodnego za zgodny. Aby zminimalizować to ryzyko należy zawęzić kryteria akceptacji o szerokość wyznaczonej szarej strefy 3:
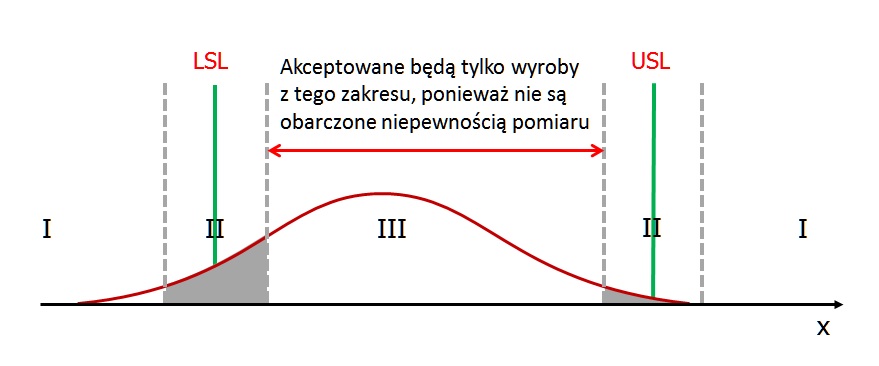
W tym momencie pojawia się pytanie, jak wyznaczyć szerokość tej strefy? Rozszerzone podejście do tematu zostało opisane np. w normie VDA 5. Jednak w naszym przypadku skorzystamy z podejścia uproszczonego, wykorzystującego właśnie wynik %GR&RTOL. Otóż wartość tego współczynnika w przybliżeniu określa procentową szerokość szarej strefy – procentową, czyli w odniesieniu do przedziału tolerancji.
Rozważmy to na konkretnym przykładzie. Przyjmijmy ponownie, że badano systemu pomiarowy, który ma służyć do oceny charakterystyki o specyfikacjach LSL=20,00 mm oraz USL=22,00 mm, czyli o przedziale tolerancji szerokości 2 mm. W wyniku obliczeń uzyskano współczynnik %GR&RTOL wynoszący 8%. Oznacza to, że szara strefa wokół granic tolerancji ma szerokość 0,16 mm, a więc konieczne jest zawężenie kryteriów akceptacji o 0,08 mm przy każdej granicy specyfikacji 4. Innymi słowy, akceptowane będą tylko te wyroby, których wynik pomiaru dał wartość w przedziale od 20,08 do 21,92. Pozostałe wyroby, których wyniki pomiaru znajdują się w przedziale tolerancji lecz jednocześnie w szarej strefie (a więc pomiędzy 20,00 i 20,08 oraz 21,92 i 22,00) powinny zostać odrzucone jako niepewne (zbyt duże jest prawdopodobieństwo, że są jednak wadliwe).
Zwróćmy uwagę, że w procesach o wysokiej zdolności problem szarej strefy w praktyce nie występuje, ponieważ nie pojawiają się wyroby, których wyniki pomiarów trafiałyby do tej strefy (pole powierzchni pod krzywą rozkładu w szarych strefach jest zbliżone do zera).
Porównanie obu wariantów
Który sposób wyliczania współczynnika %GR&R jest poprawny? Tak postawione pytanie jest nieprawidłowe, gdyż wszystko zależy od zastosowania danego systemu pomiarowego – każdy z tych współczynników może (lecz nie musi) mieć zastosowanie w różnych sytuacjach. Należy więc raczej zapytać, kiedy stosować poszczególne warianty współczynnika %GR&R i jak je interpretować.
Najprostsza odpowiedź brzmi następująco:
1) Jeżeli pomiary gromadzone przy pomocy systemu pomiarowego służą przede wszystkim do oceny zmienności procesu produkcyjnego, a w szczególności do poprawnego rozpoznawania jego rozkładu, niezbędne jest uzyskanie dobrego wyniku %GR&RTV i jednocześnie wysokiej wartości ndc. Dotyczy to zwłaszcza przypadków procesów osiągających minimalne wymagane zdolności (np. w wymaganiach klienta oczekiwana jest zdolność Cp=1,33 a proces wykazuje zdolność Cp=1,4) lub nie osiągające ich (procesów niezdolnych), ponieważ w tych przypadkach błędne rozpoznanie rozkładu procesu może prowadzić do błędnych wyliczeń współczynników zdolności a tym samym do błędnej oceny ryzyka.
2) Jeżeli pomiary gromadzone przy pomocy systemu pomiarowego służą do oceny zgodności wyrobów, niezbędne jest uzyskanie dobrego wyniku %GR&RTOL. Należy przy tym pamiętać, aby na podstawie uzyskanego wyniku zawęzić kryteria akceptacji.
W przypadku procesów o wysokiej zdolności współczynnik %GR&RTV często nie daje dobrego wyniku (powody wyjaśniono wcześniej), natomiast współczynnik %GRRTOL jest wtedy niski czyli dobry, co wynika z prostego faktu, że szerokość przedziału tolerancji TOL jest znacznie większa niż obserwowana zmienność procesu TV (patrz rysunek 2). Taki przypadek można potraktować jako dopuszczalny, czego dowodzą między innymi opisane powyżej wymagania Forda.
Z drugiej strony, w przypadku procesów o małej zdolności (poniżej 1), a więc generujących sporo sztuk wadliwych, konieczne jest uzyskanie dobrego wyniku %GR&RTOL, ponieważ w takich systemach pomiarowych interesuje nas przede wszystkim zdolność systemu pomiarowego do poprawnej oceny zgodności wyrobu. Ewentualnie dobry wynik %GRRTV jest wtedy bez znaczenia, bo mówi nam tylko, że system pomiarowy „dostrzega” zmienność bardzo słabego procesu produkcyjnego.
Na zakończenie warto jeszcze wspomnieć, że klientów VDA w zasadzie satysfakcjonuje dobry wynik współczynnika %GR&RTOL i nie wymagają oni nawet wyznaczania %GR&RTV jak również uzyskiwania wysokiego ndc. W świetle powyższego rozumowania nie powinno to jednak dziwić.
Przypisy:
1 Wyrażenie „obserwowana zmienność” jest tu używane dla odróżnienia od rzeczywistej zmienności badanych próbek PV (ang. part variation); obserwowana zmienność (TV) zawiera w sobie zarówno rzeczywistą zmienność próbek PV jak i błąd zmienności pomiaru GRR, co wynika ze wzoru.
2 W niektórych programach statystycznych, np. w programie Minitab stosowany jest skrót SV (Study Variation) co odpowiada wartości TV wyznaczonej na podstawie próbek wziętych do badania.
3 Takie wymagania są sformułowane między innymi w normie VDA 5, obowiązującej dla klientów rynku niemieckiego.
4 Szerokość strefy niepewności zmienia się wraz z zastosowaniem różnych poziomów ufności. Standardowo w tego typu analizach zakłada się poziom ufności CL=95%.





