Jednym z najważniejszych aspektów związanych ze statystycznym sterowaniem procesami (SPC) jest konieczność wyznaczania współczynników zdolności. Współczynniki te są pogrupowane parami – w każdej z takich par występuje współczynnik bez indeksu „k” oraz z indeksem „k”. W podręczniku AIAG SPC [1] opisano na przykład pary Cp i Cpk oraz Pp i Ppk. W tym artykule zajmiemy się wyjaśnieniem różnic między nimi.
Na wstępie warto zaznaczyć, że w wymaganiach rynku niemieckiego (VDA) można znaleźć jeszcze jedną parę współczynnników – Cm i Cmk. Jednak poniższe opracowanie odwołuje się do podręcznika AIAG SPC, dlatego też nie będziemy się tu nimi zajmować, skupiając uwagę na wyjaśnieniu różnic między współczynnikami Pp/Ppk oraz Cp/Cpk.
W przemyśle motoryzacyjnym dosyć powszechna jest koncepcja, zgodnie z którą współczynniki Pp/Ppk powinno się wyznaczać w fazie przedseryjnej, natomiast wraz z rozpoczęciem produkcji seryjnej powinny one zostać zastąpione przez współczynniki Cp/Cpk. Ta koncepcja, którą nazwę tu „klasyczną”, pojawia się w wymaganiach niektórych klientów. Niestety nie jest ona w pełni poprawna i nie jest zgodna z wymaganiami podręcznika AIAG SPC. Dodam też, że przedstawiona poniżej interpretacja różnic między Cp/Cpk oraz Pp/Ppk nie ma zastosowania w podejściu VDA, w którym zastosowanie obu par współczynników podlega innym regułom.
W niniejszym artykule pomijam wyjaśnienia dotyczące samego sposobu obliczania i interpretacji tych współczynników. Temat ten omówiłem dosyć dokładnie w artykule Interpretacja współczynników zdolności procesu Cp i Cpk. Jeżeli więc masz wątpliwości, co do samego sposobu ich wyznaczania, zapoznaj się wcześniej ze wspomnianą publikacją. Dla przypomnienia ograniczę się jedynie do przywołania wzorów na cztery współczynniki, będące tematem artykułu:
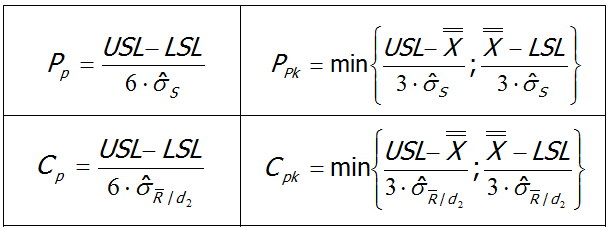
Jak widać, wzory te są prawie identyczne. Różnica pojawia się jedynie przy indeksie umieszczonym obok symbolu „sigma”. Rolą tego indeksu jest wskazanie, w jaki sposób będzie wyznaczone odchylenie standardowe (sigma) użyte we wzorze. W pierwszej kolejności przyjrzymy się wyznaczaniu sigmy dla współczynników Cp i Cpk.
Wyznaczanie odchylenia standardowego ze średniego rozstępu
We wzorze na Cp i Cpk przy wartości sigma widoczny jest indeks R/d2. Oznacza on, że odchylenie standardowe zostało wyznaczone nie z podstawowego wzoru (o którym za chwila), lecz z wzoru uproszczonego:
$$s = \frac{\bar R}{d_2}\tag{1}$$
Wartość \(\bar R\) (oznaczana czasami jako RBAR, gdzie słowo BAR zastępuje poziomą kreskę u góry) wyznaczono wyliczając średnią z podgrup, które pobierano z procesu (czym są podgrupy, wyjaśniono w artykule Interpretacja współczynników zdolności procesu Cp i Cpk). Mówimy więc, że RBAR to średni rozstęp z podgrup. Rozstęp, podobnie jak odchylenie standardowe jest miarą rozrzutu. Wartości te ze względu na odmienne podejście do ich wyznaczania są różne. Można jednak, posługując się odpowiednim współczynnikiem, przybliżyć wartość odchylenia standardowego na podstawie znanego rozstępu. I do tego celu w powyższym wzorze służy właśnie dzielnik d2. Jego wartość wynika z właściwości rozkładu normalnego (to istotna uwaga: zakładamy normalność badanego rozkładu) i jest uzależniona od liczby pomiarów w podgrupie. Wartości współczynnika d2 dla różnej wielkości podgrup można znaleźć między innymi w podręczniku AIAGSPC. Poniższa tabela przedstawia niektóre z nich:
| Wielkość podgrupy | d2 |
| 2 | 1,128 |
| 3 | 1,693 |
| 4 | 2,059 |
| 5 | 2,326 |
| 6 | 2,534 |
Wyznaczoną w ten sposób sigmę podstawiamy do wzorów na Cp i Cpk, w liczniku podajemy szerokość pola tolerancji i mamy gotowy wynik. W tym momencie dociekliwy czytelnik powinien zadać sobie pytanie: czy sigma wyznaczona uproszczonym wzorem (1) będzie taka sama, jak sigma wyznaczona wzorem podstawowym (2)? A jeżeli nie, to na czym polegają i kiedy wystąpią różnice?
Zmienność całkowita a zmienność w podgrupach
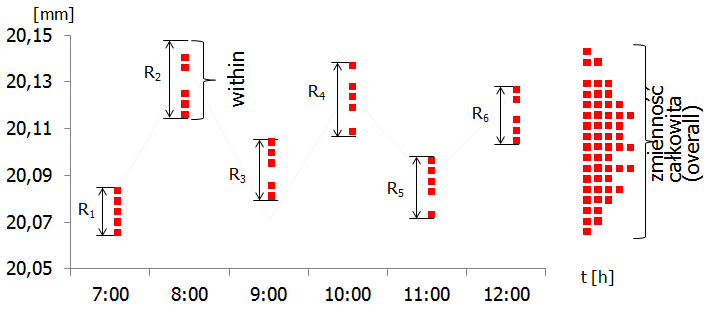
Aby to wyjaśnić, posłużymy się dwoma przykładami. W pierwszym z nich (nazwijmy go „A”) proces zachowuje się w następujący sposób: produkowane jedna po drugiej sztuki niewiele różnią się od siebie, ale w dłuższej perspektywie czasowej w procesie występują znaczące przesunięcia. Załóżmy, że do wyznaczania współczynników Cp,Cpk pobiera się podgrupy po 5 kolejnych sztuk co 1 godzinę. Kolejne sztuki są produkowane w tempie 1 sztuka co 15 sekund, a więc obejmują krótki odcinek czasu (75 sekund), podczas gdy czas upływający między poszczególnymi podgrupami to w przybliżeniu 3600 sekund. Sytuację obrazuje poniższy rysunek:
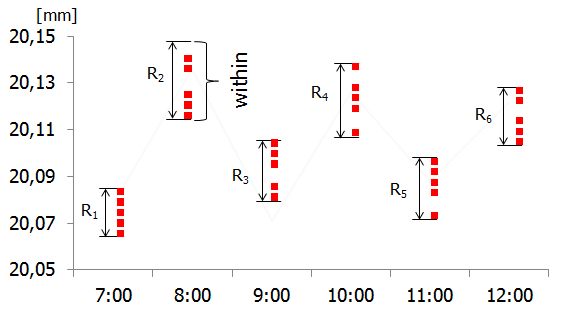
Wróćmy teraz do wzoru (1) i zadajmy sobie pytanie, czy zaobserwowane różnice między grupami (ang. between variability) wpłyną na wyliczoną za jego pomocą wartość sigma? Oczywiście, że nie – w tym wzorze występuje jedynie wartość średniego rozstępu w podgrupach (ang. within variability), który jest stosunkowo mały i wzór (1) jest niewrażliwy na ewentualne różnice w położeniu samych podgrup.
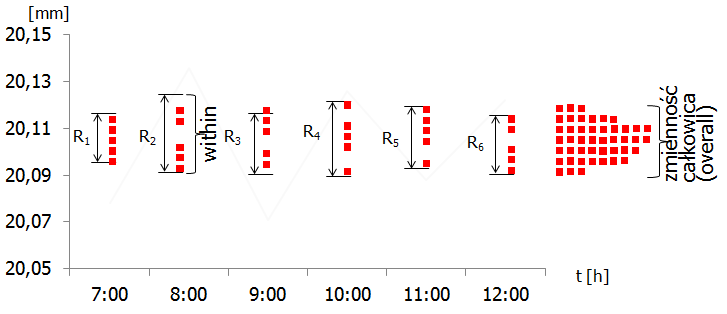
Żeby to lepiej zrozumieć spójrzmy na kolejny przykład (nazwiemy go B), w którym nie występuje zjawisko „pływania procesu”, a więc poszczególne podgrupy znajdują się na podobnej wysokości wykresu (średnie z podgrup mają podobną wartość).
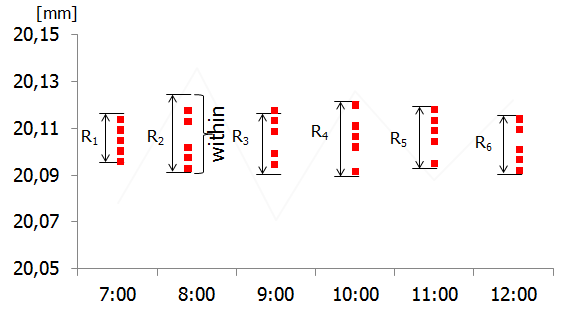
Zakładając, że średni rozstęp w podgrupach jest taki sam jak w przykładzie A, wartość RBAR będzie w obu przypadkach identyczna, co z kolei da w wyliczeniach taką samą sigmę i w konsekwencji takie same współczynniki Cp i Cpk. A przecież procesy A i B znacząco się różnią! Innymi słowy, współczynniki Cp i Cpk nie uwzględniają zmienności between, a więc nie pokazują globalnej (ang. overall) zmienności procesu.
Pp, czyli gdzie jest (P)ies (p)ogrzebany
Zadajmy sobie kolejne pytanie. Co by się stało, gdybyśmy na chwilę zapomnieli o podgrupach i wrzucili wyniki wszystkich pomiarów do jednego worka? Na przykład gdybyśmy potraktowali tak nasz zbiór danych (załóżmy, że ma on 30 podgrup po 5 pomiarów, co daje w sumie 150 indywidualnych odczytów), a następnie obliczyli odchylenie standardowe posługując się wzorem podstawowym:
Wzór ten nie będzie „wiedział”, z której podgrupy pochodzą poszczególne wyniki, a więc potraktuje je łącznie i „zauważy” znaczne różnice występujące pomiędzy pomiarami. Krótko mówiąc, wyliczone w ten sposób odchylenie standardowe oprócz zmienności within (obserwowanej w obrębie podgrup) uwzględni w wyliczeniach również zmienność between (występującą między podgrupami). W rezultacie w przykładzie A sigma liczona wzorem uproszczonym (1) będzie znacząco niższa niż sigma liczona wzorem podstawowym (2).
Analogiczne rozumowanie możemy przeprowadzić dla przykładu B. Jednak w tym przypadku, ponieważ nie występuje zmienność między podgrupami, sigma z wzoru (1) będzie zbliżona do sigmy z wzoru (2).
Po tych wyjaśnieniach nadszedł czas na najważniejszą obserwację – sigma wyliczona wzorem (2) jest sigmą, którą stosuje się do wyznaczania współczynników Pp i Ppk.
W powyższych rozważaniach pojawiło się tu wiele interesujących i nowych informacji, spróbujmy podsumować uzyskany scenariusz postępowania:
1) Z procesu pobieramy po kilka sztuk (w omawianym przykładzie 5) i mierzymy każdą z nich. Uzyskane wyniki tworzą jedną podgrupę.
2) Co jakiś czas (w przykładzie co 2 godziny) powtarzamy tę czynność, uzyskując w rezultacie n podgrup.
3) Stosując wzór (1) obliczamy odchylenie standardowe dla zebranych danych i na tej podstawie wyznaczamy współczynniki Cp i Cpk.
4) Stosując wzór (2) obliczamy drugie odchylenie standardowe i za jego pomocą wyznaczamy Pp i Ppk.
Jeżeli między uzyskami współczynnikami (Cp-Pp oraz Cpk-Ppk) zaobserwujemy znaczące różnice, oznacza to, że w procesie występuje zmienność typu between. Innymi słowy, występują w nim przyczyny specjalne, które powodują niestabilność średniej procesu. Z drugiej strony, jeżeli współczynniki te są sobie równe (Cp=Pp i odpowiednio Cpk=Ppk), to możemy stwierdzić, że w procesie nie występuje zmienność typu between, a więc jest on stabilny z punktu widzenia jego położenia.
Wnioski końcowe
Jakie najważniejsze przesłanie wynika z tych rozważań? Otóż, współczynniki zdolności Cp i Cpk rozpatrywane w oderwaniu od pozostałych dwóch mogą powodować mylną ocenę procesu, zwłaszcza jeżeli zachowuje się on tak, jak opisano to w przykładzie A. W takiej sytuacji może się zdarzyć, że Cp i Cpk będą na wystarczającym poziomie, podczas gdy rzeczywista wydajność procesu (a więc Pp i Ppk) będzie niezadowalająca. Tak więc aby poznać rzeczywistą wydajność procesu, konieczne jest wyznaczenie z tych samych danych jednocześnie współczynników Cp,Cpk oraz Pp,Ppk. Dopiero ta ostatnia para da nam informację o rzeczywistej wydajności procesu (ang. process performance, czyli Pp).
Z drugiej strony, dzięki wyznaczeniu Cp,Cpk jesteśmy w stanie ocenić potencjał procesu, który jest możliwy do osiągnięcia przy założeniu, że proces zostanie ustabilizowany pod względem położenia (czyli zostanie zredukowana zmienność typu between). Wniosek końcowy jest więc następujący: oceniając zdolność procesu w produkcji seryjnej nie wystarczy wyznaczać współczynników Cp i Cpk, ale koniecznym jest również wyliczanie z tych samych danych współczynników Pp i Ppk, ponieważ dopiero wszystkie cztery dają nam pełny obraz procesu. Analogiczne wnioski, choć wyrażone innymi słowami, przedstawia również podręcznik SPC [1]: Współczynnik Cpk jest przydatny do stwierdzenia, czy proces ma potencjał (ang. is capable) do spełnienia wymagań klienta […]. Z kolei współczynnik wydajności Ppk (ang. performance) pokazuje, czy proces faktycznie je spełnia.
Bibliografia
[1] Statistica Process Controll, AIAG, 2005





