W ocenie jakości procesu coraz powszechniej wykorzystuje się wskaźniki zdolności (Cp/Cpk, Pp/Ppk). Jednocześnie trzeba pamiętać, że do poprawnego ich wyznaczenia konieczny jest dobór odpowiedniego modelu rozkładu statystycznego. Jest to ważny punkt, ponieważ zastosowany model ma wpływ na wartości współczynników. Te z kolei są narzędziem do oceny ryzyka w procesie lub, mówiąc inaczej, pokazują nam prawdopodobieństwo wyprodukowania wyrobów poza specyfikacją. Oznacza to, że zastosowanie źle dopasowanego modelu może prowadzić do błędnej oceny ryzyka a w konsekwencji do niepodejmowania działań zapobiegawczych w procesach, w których należałoby je wprowadzić lub przeciwnie – do adresowania niepotrzebnych działań w stosunku do procesów nie stwarzających zagrożeń jakościowych.
W praktyce poszukiwanie modelu rozkładu jest realizowane w dwóch krokach:
- Wykonanie testu normalności dla badanego zbioru danych.
- Jeżeli test normalności dał negatywny wynik (odrzucono hipotezę zerową o tym, że próbka pochodzi z populacji o rozkładzie normalnym), następuje próba dopasowania innego modelu rozkładu statystycznego lub znalezienia transformacji, która przekształca dane do rozkładu normalnego.
Doświadczeni specjaliści zarządzający procesami, którzy prowadzą takie analizy, zdają sobie sprawę, że w bardzo wielu przypadkach oba kroki dają negatywny wynik. Innymi słowy, następuje odrzucenie hipotezy o normalności rozkładu i jednocześnie nie udaje się znaleźć innego modelu parametrycznego lub transformacji, które pozwoliłyby wiarygodnie wyznaczyć współczynniki zdolności.
Model rozkładu jest parametryczny, jeśli jego kształt jest całkowicie określony przez skończoną liczbę parametrów. Oznacza to, że cała struktura rozkładu może być opisana za pomocą kilku liczb, takich jak średnia, wariancja czy skośność. Rozkładem parametrycznym jest np. rozkład normalny, który jest jednoznacznie definiowany za pomocą dwóch parametrów – średniej i odchylenia standardowego.
Podręczniki w takiej sytuacji zwykle sugerują (słusznie), że niemożność dopasowania parametrycznego modelu rozkładu oznacza brak stabilności procesu, a następnie zalecają poprawę procesu, ponowne zebranie danych i powtórną analizę.
Czy zawsze warto dzielić włos na czworo?
Tyle teorii, jednak w praktyce mogą pojawiać się scenariusze, w których poszukiwanie dopasowanego modelu rozkładu nie daje korzyści w postaci lepszej oceny ryzyka. Takim przypadkiem są procesy o wysokiej zdolności. Za wysoką zdolność możemy przyjąć Ppk > 2.
Wyobraźmy sobie następujący przykład – w procesie toczenia wytwarzana charakterystyka ma tolerancje LSL = 19,95 mm i USL=20,45 mm. Proces jest realizowany na maszynie CNC, co sprawia, że zaobserwowane wyniki znajdują się w przedziale od 20,126 mm do 20,252 mm a 6*sigma tego procesu wynosi 0,220 mm, a więc proces „wykorzystuje” tylko około 44% przedziału tolerancji. Na podstawie tych informacji łatwo można oszacować, że zdolność Pp takiego procesu (przy założeniu normalności rozkładu) wynosi nieco ponad 2.
Opisany scenariusz przedstawia przykładowy histogram takiego procesu wraz z dopasowaną krzywą rozkładu normalnego.
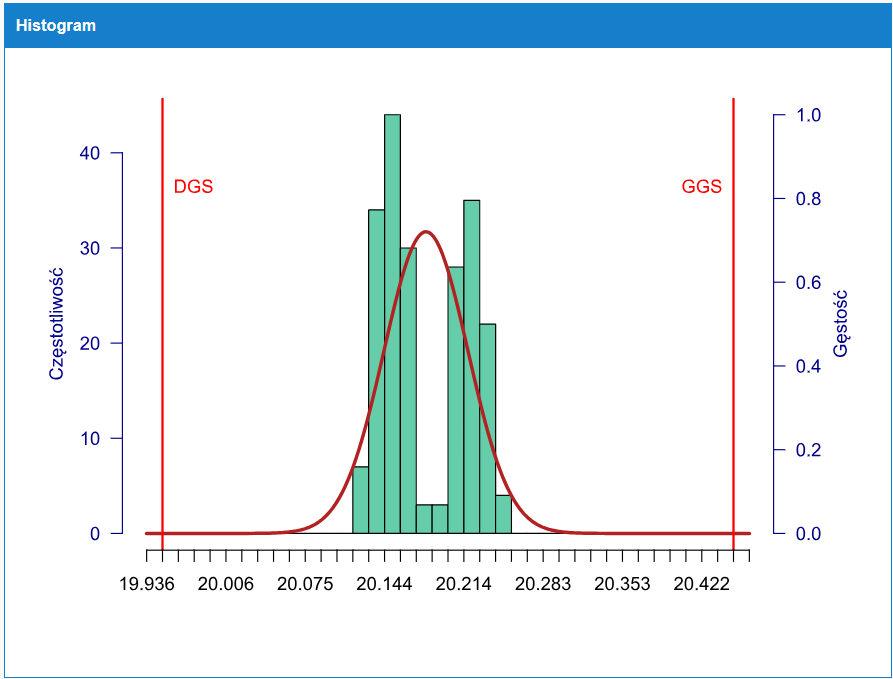
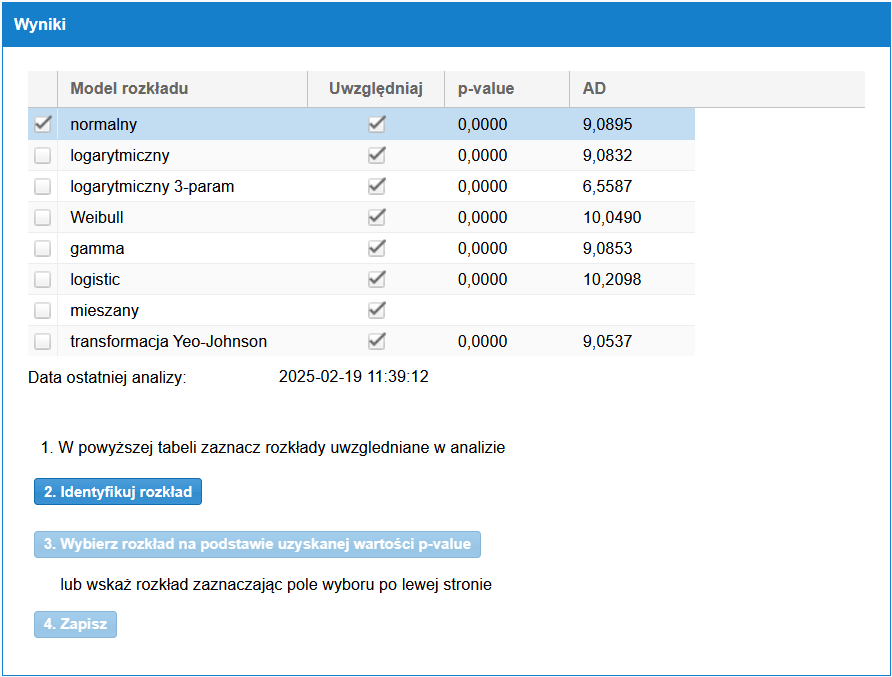
Kształt histogramu wyraźnie sugeruje, że mamy do czynienia z rozkładem wielomodalnym (dwa wierzchołki), co potwierdza test normalności – dla przedstawionego zestawu danych w teście Anderson-Darling uzyskano wartość p-value poniżej poziomu alfa=5%. Próby dopasowania do innych parametrycznych modeli rozkładu też okazały się nieskuteczne (rysunek 2), więc zgodnie z przedstawioną na początku koncepcją, należałoby teraz dążyć do ustabilizowania procesu, co z kolei powinno doprowadzić do wyeliminowania wielomodalności, czyli prawdopodobnie będzie wtedy możliwe znalezienie jakiegoś modelu parametrycznego.
Warto dostrzec również inną prawidłowość. Jeżeli obserwujemy niewielką zmienność procesu, oznacza to, że oddziaływanie przyczyn ogólnych jest relatywnie małe w odniesieniu do przedziału tolerancji. Może to prowadzić do ujawniania się przyczyny specjalnych wpływających na kształt rozkładu (a więc np. powodujących wielomodalność), które pozostałyby ukryte (nieistotne) w przypadku większej zmienności ogólnej. Innymi słowy, im lepszy proces pod względem minimalizacji przyczyn ogólnych, tym większe potencjalne oddziaływanie przyczyn specjalnych a tym samym większe zakłócenia w rozkładzie procesu. Często dochodzi do paradoksalnej sytuacji, że w mniej kontrolowanym procesie (z większą zmiennością ogólną), testy statystyczne będą wykazywać normalność (lub inny model), natomiast w wyniku doskonalenia procesu dojdzie do ujawnienia się istniejących ale dotychczas mniej istotnych przyczyn specjalnych. W efekcie proces, który dotychczas „zaliczał” test normalności, zacznie dawać negatywny wynik.
Pytanie jednak, czy działania zmierzające do usuwania takich przyczyn specjalnych są ekonomicznie uzasadnione w odniesieniu do potrzeb jakościowych? Pamiętajmy, że klienta przede wszystkim interesuje, aby charakterystyka wyrobu znalazła się w zdefiniowanych specyfikacjach. Z drugiej strony przy tak małej zmienności procesu w stosunku do tychże specyfikacji niezależnie od przyjętego modelu rozkładu szacowane ryzyko pojawienia się wyników poza specyfikacją jest bliskie zeru. Na przykład w rozkładzie normalnym jeżeli Pp=Ppk=2 szansa na pojawienie się wyniku poza specyfikacją wynosi około 0,002 ppm, co oznacza, że taki wynik może pojawić się 1 raz na 500 milionów wyprodukowanych wyrobów. Gdybyśmy dla tych samych danych próbowali użyć innych modeli rozkładu, zarówno parametrycznych jak i nieparametrycznych (np. rozkład mieszany), szacowany poziom ryzyka nie ulegałby wielkiej zmianie.
Co to oznacza w praktyce? Otóż im mniejsza zmienność procesu w stosunku do przedziału tolerancji (za umowną granicę można przyjąć zdolność Ppk>2), tym poprawne dopasowanie rozkładu ma mniejsze znaczenie w odniesieniu do oszacowania ryzyka w procesie. W takich przypadkach, gdy nie udaje się dopasować żadnego modelu, można więc bezpiecznie przyjmować rozkład normalny, mimo, że nie udało się potwierdzić hipotezy, że analizowane dane pasują do tego modelu.
Przyjęcie takiego rozumowania i wdrożenie go w wewnętrznych procedurach organizacji może być dużym udogodnieniem, bo pozwoli uniknąć niepotrzebnych dyskusji i „tłumaczenia się” czy to przed klientem, czy audytorem, dlaczego proces nie ma rozkładu normalnego i dlaczego nie udało się dopasować innego modelu. Po prostu próba eliminacji zaobserwowanych przyczyn specjalnych w takich przypadkach byłaby typową nadjakością (ang. overquality).
Empirycznym dowodem na takie wnioskowanie mogą być wyniki oceny zdolności uzyskane na wspomnianych danych, przy zastosowania różnych modeli rozkładu (żaden z nich nie dał pozytywnego wyniku testu dopasowania). Ostatni wynik uzyskano po zastosowaniu nieparametrycznego rozkładu mieszanego. Ten rozkład najlepiej odwzorowuje kształt histogramu (jest optymalnie dopasowany do danych) i tym samym można uznać, że najwierniej odzwierciedla zdolność a tym samy ryzyka w tym procesie (przy założeniu, że zaobserwowany rozkład jest powtarzalny, czyli nie zmienia się w czasie).
| Model rozkładu | Pp | Ppk |
| normalny | 2,28 | 2,10 |
| logarytmiczno normalny | 2,27 | 2,10 |
| mieszany | 3,13 | 2,96 |
Z uzyskanych wyników można wyciągnąć również wniosek, że wartości zdolności dla rozkładów parametrycznych (a więc jednomodalnych) dają bardziej pesymistyczne wyniki niż w przypadku rozkładu mieszanego. Innymi słowy, gdy zostaje przyjęty jednomodalny rozkład parametryczny, prowadzi to do przeszacowania rozrzutu procesu. Dlatego tym bardziej wyznaczanie zdolności przy założeniu normalności w takim zestawie danych nie powoduje niedoszacowania ryzyka w tym procesie, a wręcz przeciwnie – doprowadza do jego przeszacowania.
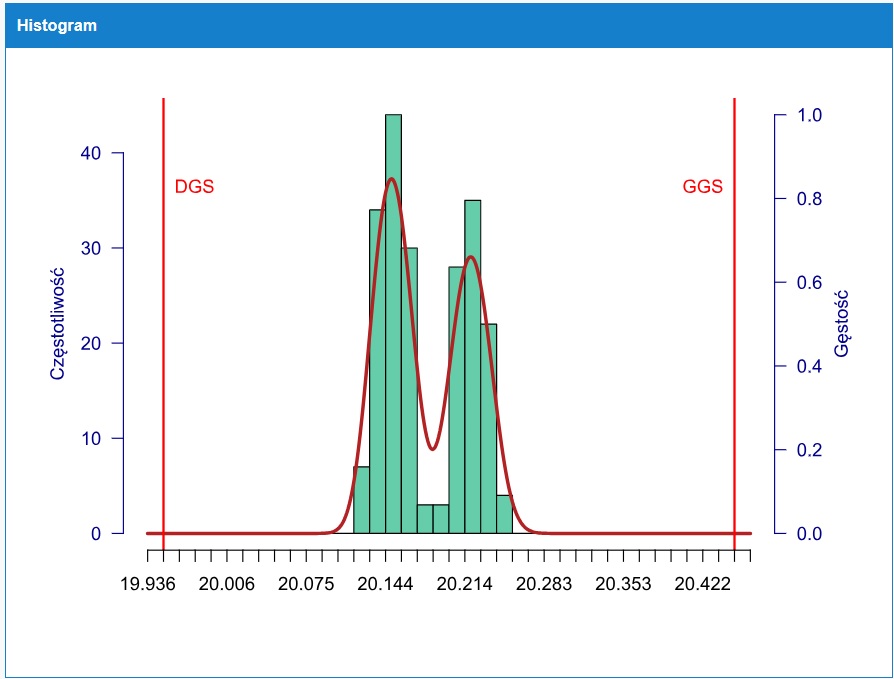
Więcej informacji na temat programu proCONTROL i jego zastosowaniu do prowadzenia bieżących analiz SPC w procesach znajdziesz w tym linku.
Piotr Stokłosa




