Potrzeba badania współczynników zdolności procesu jest w przemyśle motoryzacyjnym powszechnie znana. Typowym wymaganiem klienta jest, aby dostawca osiągał pewne minimalne poziomy zdolności procesu dla wybranych charakterystyk, w szczególności dla charakterystyk specjalnych.
Zwykle operuje się tu trzema progami: 1,33, 1,67 oraz 2,0.
Niestety, w wielu przedsiębiorstwach za wyznaczaniem współczynników zdolności nie idzie w parze ich zrozumienie. A szkoda, gdyż we wspomnianych wskaźnikach kryje się wiele informacji o procesie, które odpowiednio wykorzystane mogą się stać cennym narzędziem do sterowania nim i jego doskonalenia.
Dodatkowa trudność wynika z faktu, że wspomnianych współczynników jest w sumie 6. Tworzą one trzy pary: Cm i Cmk, Pp i Ppk, Cp i Cpk. Można do nich zaliczyć jeszcze jedną parę, Cg i Cgk, służącą jednak nie do oceny samego procesu, ale systemu pomiarowego. Dlatego żeby uprościć nasze rozważania wyjaśnijmy na początku kluczową kwestię – różnica między poszczególnymi parami współczynników sprowadza się przede wszystkim do sposobu i czasu zbierania danych oraz metody wyliczania odchylenia standardowego. Jeżeli zaś chodzi o interpretację uzyskiwanych wyników (za wyjątkiem Cg i Cgk, ale te współczynniki nie są przedmiotem tego artykułu), jest ona praktycznie identyczna.
Skupimy się więc na najpopularniejszej parze współczynników Cp i Cpk, mając na uwadze, że wszystkie przedstawione poniżej wnioski można odnieść również do par Cm i Cmk oraz Pp i Ppk.
Współczynnik Cp
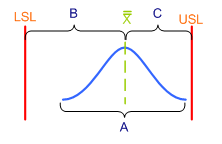
Współczynnika Cp nie sposób zrozumieć bez zaprezentowania wzoru, który służy do jego wyliczania. Wzór zaś najlepiej zrozumiemy, jeżeli zestawimy go z rysunkiem przedstawiającym przykładowy proces w odniesieniu do pewnych tolerancji.

Zacznijmy od wyjaśnienia wszystkich składników wzoru. USL to Upper Specification Limit, a więc górna granica tolerancji (GGT) lub górna granica specyfikacji (GGS). Analogicznie, LSL to Lower Specification Limit, czyli dolna granica tolerancji (DGT) lub dolna granica specyfikacji (DGS). Wartości te pochodzą ze specyfikacji klienta i wstawia się je do wzoru odczytując je z rysunku technicznego lub z innej dokumentacji. Upraszczając sprawę możemy więc powiedzieć, że licznik przedstawionego wzoru, czyli wyrażenie USL – LSL to tzw. „szerokość pola tolerancji”. Na powyższym rysunku obie granice zostały oznaczone czerwonymi pionowymi kreskami.
Wyrażenie zawarte w mianowniku wymaga nieco dokładniejszego wyjaśnienia. Zapis 6*σ oznacza, że we wzorze umieszczamy wartość odpowiadającą sześciu odchyleniom standardowym, jakie wyliczono na podstawie zebranych danych. W tym celu wcześniej dokonano odpowiedniej liczby pomiarów (słowo „odpowiedniej” jest tu dużym uproszczeniem – o liczbie pomiarów decydują ściśle określone reguły), z których wyliczono odchylenie standardowe. Sposób wyliczania odchylenia standardowego w tym wzorze zostanie omówiony w oddzielnym artykule. W tej chwili przyjmijmy więc, że wyliczone tu odchylenie standardowe jest po prostu miarą rozrzutu uzyskanych wyników pomiaru. Innymi słowy, odchylenie standardowe mówi nam, jak bardzo różnią się między sobą uzyskane wyniki. Zależność jest tutaj dosyć prosta – im bardziej wyniki pomiarów różnią się od siebie, tym większy rozrzut i tym większe odchylenie standardowe. Odnosząc to spostrzeżenie do wymagań produkcyjnych, każdy powinien się zgodzić, że zależy nam na tym, aby poszczególne wyniki pomiarów jak najmniej różniły się między sobą, gdyż jest to dowodem na powtarzalność uzyskiwanych charakterystyk. A więc im mniejsze odchylenie standardowe, tym lepiej. Na powyższym rysunku niebieski fragment krzywej odpowiada zakresowi 6*sigma.
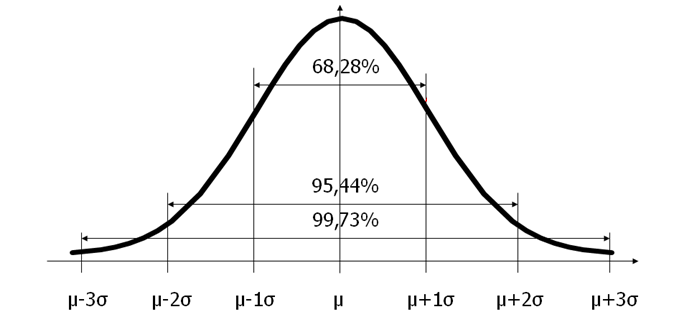
W tym miejscu pojawia się kolejne pytanie: dlaczego we wzorze sigma jest pomnożona przez 6? Otóż jest tu ukryta pewna prawidłowość, która wiąże się z właściwościami rozkładu normalnego. Tak zwana reguła empiryczna dotycząca tego rozkładu stwierdza, że dla idealnego, teoretycznego rozkładu normalnego:
- – w odległości +/- 1*odchylenie standardowe od wartości średniej znajduje się około 67% wszystkich uzyskanych wyników
- – w odległości +/- 2*odchylenie standardowe od wartości średniej znajduje się około 95% wszystkich uzyskanych wyników
- – w odległości +/- 3*odchylenie standardowe od wartości średniej znajduje się około 99,73% wszystkich uzyskanych wyników
Na podstawie poczynionych do tej pory spostrzeżeń możemy więc powiedzieć, że współczynnik Cp mówi nam, jaki jest stosunek szerokości przedziału tolerancji (obszar B z rysunku 1) do sześciu odchyleń standardowych naszego procesu (obszar A z rysunku 1), a więc do obszaru, w którym znajduje się około 99,73% uzyskanych wyników pomiarów jakiejś charakterystyki.
Warto również zwrócić uwagę na inną, głębszą implikację tego stwierdzenia. Wspomniana powyżej reguła empiryczna dotyczy rozkładu normalnego (opisywanego krzywą Gaussa). Jeżeli jednak nasz rozkład nie ma cech rozkładu normalnego (co zdarza się dosyć często), przyjęcie tej reguły może prowadzić do błędnych wyliczeń współczynnika zdolności, bo w obszarze 6*sigma nie będzie się znajdowało 99,73% wyników.
Spróbujmy kontynuować analizę wzoru z rysunku 1. Przedstawiona tam krzywa dzwonowa jest lekko przesunięta w prawo. Wyobraźmy sobie teraz, że przesuwamy ją w prawo coraz bardziej, na przykład do stanu przedstawionego poniżej:
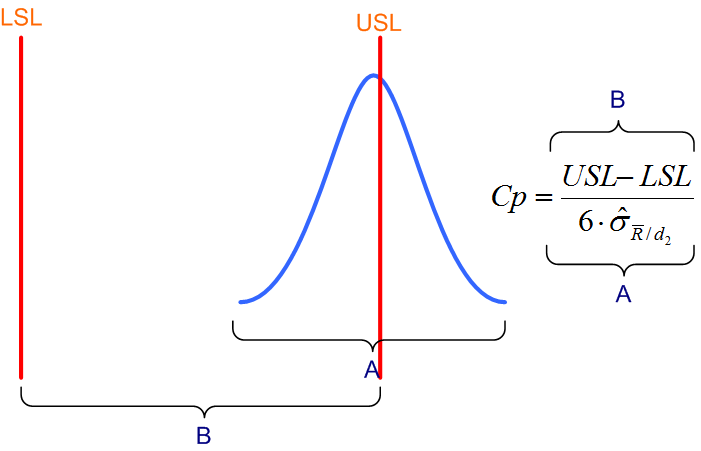
Na pierwszy rzut oka widać, że prawie połowa zmierzonych wyrobów (pamiętajmy, że krzywa rozkładu powstaje w wyniku utworzenia histogramu, który odzwierciedla częstość występowania charakterystyk o określonym wymiarze) jest poza specyfikacją, a więc, że poziom wadliwości zbliża się do 50%. Możemy sobie nawet wyobrazić sytuację, że pokazana na rysunku krzywa dzwonowa całkowicie przesunie się poza tolerancje i będziemy produkować prawie wyłącznie wadliwe wyroby.
Zadajmy więc sobie teraz pytanie, jak to przesunięcie wpłynie na wartość współczynnika Cp? Aby uzyskać odpowiedź, musimy ponownie spojrzeć na wzór. Jego licznik nie ulegnie zmianie, bo przecież granice specyfikacji nie zmieniły się. Jedynym zmiennym elementem mianownika jest natomiast sigma, która odzwierciedla rozrzut. Ale jeżeli założymy, że kształt rozpatrywanej krzywej nie ulega zmianie (przesuwamy ją tylko w prawo), musimy się zgodzić, że i rozrzut tej zmianie nie uległ, a więc sigma pozostaje taka sama. Wypływa stąd wniosek: niezależnie od położenia krzywej rozkładu, jeżeli rozrzut (czyli sigma) nie ulega zmianie, wartość współczynnika Cp nie zmieni się. Innymi słowy może zdarzyć się tak, że dzięki małemu rozrzutowi będziemy uzyskiwali bardzo wysoki (a więc dobry) współczynnik Cp i jednocześnie będziemy produkować prawie wyłącznie wadliwe (bo poza specyfikacją) wyroby.
W przedstawionym przykładzie intuicyjnie zauważymy również, że ryzyko wyprodukowania wadliwego wyrobu jest tym mniejsze, im lepiej wyśrodkowany jest proces, ponieważ z każdej strony jesteśmy wtedy równie daleko od granic specyfikacji. Każde wahnięcie w wyśrodkowaniu procesu grozi przesunięciem się w stronę dolnej lub górnej granicy specyfikacji a więc spowoduje wzrost ryzyka, że część wyrobów znajdzie się poza specyfikacją. Jak więc sprawdzić, czy oprócz dobrego rozrzutu proces jest również dobrze wyśrodkowany? Odpowiedzi na to pytanie udziela drugi współczynnik, czyli Cpk.
Współczynnik Cpk
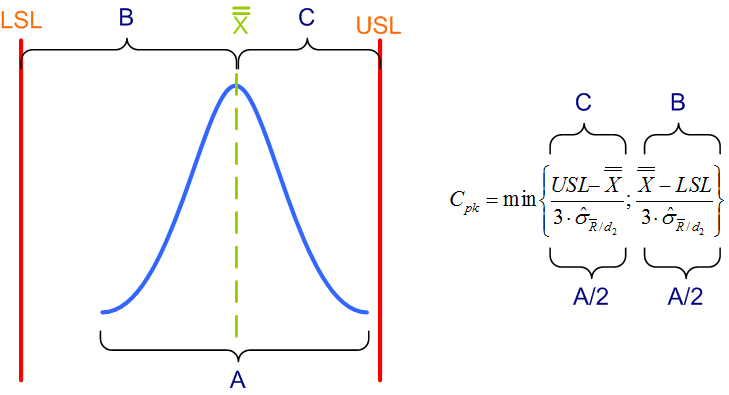
Również w przypadku Cpk najprościej zacząć od prezentacji graficznej. Na przedstawionym poniżej rysunku pojawił się nowy element – pionowa przerywana linia oznaczająca średnią z procesu. W przypadku współczynnika Cpk jest to tak zwana średnia ze średnich (dlatego dwie poziome kreski nad X).
Wyliczanie średniej ze średnich odbywa się następująco. Załóżmy, że w trakcie prowadzenia karty kontrolnej co 2 godziny są pobierane próbki składające się z 5 sztuk. Razem tworzą one tzw. podgrupę. A więc w jednej podgrupie uzyskujemy pięć pomiarów. Z nich wylicza się średnią. Średnia ta jest wyliczana również w każdej kolejne podgrupie, a więc po pewnych czasie mamy pewien zbiór średnich. Jeżeli następnie z nich wyliczymy kolejną średnią, uzyskamy wspomnianą średnią ze średnich.
W rozkładzie normalnym można przyjąć, że średnia ze średnich odpowiada środkowi procesu, a więc może być miarą jego położenia. W najprostszym przypadku, jeżeli wartość nominalna danej charakterystyki leży w środku specyfikacji, możemy powiedzieć, że im średnia procesu jest dalej od tej wartości nominalnej, tym gorzej. Dlaczego? Wyjaśniliśmy to już na końcu poprzedniego podrozdziału.
Czas teraz spojrzeć na wzór do obliczania Cpk. Na pierwszy rzut oka wydaje się bardziej skomplikowany niż wzór na Cp, jednak po analizie dojdziemy do wniosku, że to w zasadzie ten sam wzór, jedynie nieco zmodyfikowany.
Po pierwsze zauważmy, że nie jest to jeden wzór a dwa (na rysunku wskazane przez klamry B i C). Wyznaczamy więc dwie niezależne wartości, a następnie wybieramy z nich mniejszą, o czym informuje nas wyrażenie min. Przyjrzyjmy się pierwszemu wzorowi: w liczniku od górnej granicy specyfikacji (USL) odejmujemy średnią procesu, a następnie dzielimy wszystko przez 3*sigma. W drugim wzorze wykonujemy analogiczne wyliczenia, ale tym razem w liczniku bierzemy obszar od średniej do dolnej graniczy specyfikacji (LSL) i również dzielimy wynik przez 3*sigma. Jak łatwo się domyślić, dzielimy oba wyrażenia przez 3*sigma a nie przez 6*sigma, ponieważ całą krzywą rozkładu podzieliliśmy na 2 części.
Po uzyskaniu obu wyników wybieramy z nich mniejszy (wyrażenie „min”). Dlaczego mniejszy? Odpowiedzi udziela nam znowu poprzedni rysunek. Ponieważ pokazany na nim rozkład jest przesunięty nieco w stronę górnej granicy specyfikacji, obszar C jest krótszy od obszaru B. To z kolei powoduje, że pierwszy wzór (oznaczony klamrą C) da mniejszy wynik niż drugi (oznaczony klamrą B). Jednocześnie widzimy, że przesunięcie procesu w stronę GGS wiąże się z większym ryzykiem jej przekroczenia. Dlatego właśnie z obu uzyskanych wyników wybieramy mniejszy, gdyż to on pokazuje nam większe ryzyko wyjścia poza specyfikację.
Zaopatrzeni w tę wiedzę możemy teraz śmielej interpretować wyniki uzyskiwane w procesach. Najlepiej wyjaśni to kilka przykładów:
| Cp | Cpk | Interpretacja |
| 2 | 2 | Proces wysoko zdolny i dobrze wyśrodkowany. Przypadek idealny. |
| 2 | 0,5 | Proces o dużym potencjale (Cp), ale słabo wyśrodkowany (niskie Cpk). Należy poprawiać wyśrodkowanie. |
| 0,5 | 0,5 | Proces dobrze wyśrodkowany (Cp=Cpk), ale o bardzo dużym rozrzucie. Należy zmniejszać rozrzut. |
| 1,8 | -0,5 | Proces o dużym potencjale, ale na skutek złego wyśrodkowania większość wyników będzie poza specyfikacją (średnia procesu jest poza jedną z granic specyfikacji). |
Za pomocą powyższej tabeli można również wytłumaczyć terminologię odnoszącą się do obu współczynników. Cp często nazywa się zdolnością potencjalną, ponieważ wskazuje, co można uzyskać z procesu, jeżeli zostanie idealnie wyśrodkujemy. Z kolei Cpk nazywa się zdolnością rzeczywistą, bo informuje o rzeczywistym poziomie wadliwości, jaki prawdopodobnie wystąpi w związku ze zbyt dużym rozrzutem oraz niewłaściwym wyśrodkowaniem procesu.
Kierunek przesunięcia – współczynniki Cpl i Cpu
Dysponując wartościami Cp oraz Cpk i potrafiąc je interpretować, możemy dokonywać regulacji procesu. Niskie Cp będzie ostrzegało o dużym rozrzucie. Z kolei niskie Cpk w stosunku do wysokiego Cp będzie informowało słabym wyśrodkowaniu. W tym ostatnim przypadku pojawi się jednak pytanie: niskie Cpk to niewłaściwe wyśrodkowanie, ale w którą stronę jest przesunięty proces? Jeżeli jeszcze raz spojrzymy na wzór na Cpk zauważymy, że informacja o kierunku przesunięcia procesu jest widoczna zanim wybierzemy wartość minimalną. Jeżeli pierwszy człon daje niższy wynik niż drugi – proces jest przesunięty w prawo. Jeżeli pierwszy człon daje wynik wyższy od drugiego – proces jest przesunięty w lewo. Po wyznaczeniu minimum tracimy tę informację. Z tego względu w większości narzędzi informatycznych służących do obliczania współczynników zdolności podawane są jeszcze dwie wartości pomocnicze: Cpu i Cpl, będące niczym innym, jak wartościami wyznaczanymi przez wzory cząstkowe z formuły na Cpk – Cpu to wartość wyrażenia z USL w liczniku, natomiast Cpl to wartość wyrażenia z LSL. W ten sposób uzyskujemy zestaw czterech współczynników: Cp, Cpk, Cpu i Cpl, dzięki którym świadomy pracownik jest w stanie odczytać wiele sygnałów dochodzących z procesu i odpowiednio na nie zareagować.





