W przemyśle motoryzacyjnym i nie tylko dosyć powszechne jest wyznaczanie zdolności procesowych za pomocą arkuszy kalkulacyjnych. Najczęściej, choć z moich obserwacji wynika, że praktycznie w stu procentach przypadków, do tego celu używa się „klasycznych” wzorów, w których rozrzut procesu jest opisywany za pomocą wartości 6*sigma. Czy jednak takie podejście zawsze jest prawidłowe? Okazuje się, że nie.
„Klasyczne” wzory na obliczanie zdolności
Zacznijmy od przypomnienia wspomnianych klasycznych (choć w zasadzie należałoby je nazwa „szczególnymi”, ponieważ dotyczą pewnego szczególnego przypadku, o czym za chwilę) wzorów na współczynniki Cp/Cpk lub Pp/Ppk (opis różnic między współczynnikami Cp i Pp znajdziesz tutaj; w kontekście tego artykułu wspomniane różnice są nieistotne).
| $$Cp, Pp = \frac{USL-LSL}{6 \cdot s}\tag{1}$$ | $$Cp_k, Pp_k = \text{min}\Big\{\frac{USL-{\bar{\bar x}}}{3 \cdot s};\frac{{\bar{\bar x}}-LSL}{3 \cdot s}\Big\}\tag{2}$$ |
Wzór (1) informuje o stosunku tolerancji (USL – LSL) do przedziału zmienności procesu, wyrażonego poprzez wartość 6*s (gdzie s oznacza odchylenie standardowe, nazywane dalej sigmą). Podręcznik AIAG SPC definiuje to zgrabnie jako relację „głosu klienta”, czyli wymagań specyfikacji, do „głosu procesu”, czyli rozrzutu wyników wyrażonego poprzez odchylenie standardowe. Podobną zależność prezentuje wzór (2), dochodzi tu jednak jeszcze ocena położenia procesu.
Wspomniane wzory został opracowane z wykorzystaniem pewnej ważnej zależności, nazywanej w statystyce regułą 68-95-99,73. Reguła ta odnosi się do oczekiwanego procentu wyników, jakiego należy oczekiwać w pewnym przedziale funkcji gęstości rozkładu normalnego, uwzględniając całkowite wielokrotności odchylenia standardowego, odejmowane lub dodawane względem średniej procesu. Innymi słowy, jeżeli znamy położenie procesu (najczęściej wyrażane średnią z wszystkich pomiarów) oraz jego odchylenie standardowe, to niezależnie od konkretnych wartości, będą obowiązywały następujące zależności:

Należy pamiętać, że przedstawiony powyżej wykres jest funkcją gęstości prawdopodobieństwa (pdf – probability density function), a więc wyróżnione przedziały określają zakres całkowania (np. od -1*sigma do +1*sigma), natomiast zaprezentowana wartość procentowa (np. 68,28%) odzwierciedla wynik tego całkowania, podając odpowiadający danemu przedziałowi zakres pola powierzchni pod funkcją gęstości (całkowita powierzchnia pola pod tą krzywą wynosi 1, czyli 100%, co odpowiada prawdopodobieństwu całkowitemu).
Jak liczyć zdolności w przypadku innych modeli rozkładu?
W poprzednich akapitach udało się mi przemycić jedno ważne założenie – przyjąłem mianowicie, że rozkład jest normalny. Dlaczego to takie ważne? Ponieważ w rozkładzie normalnym rozrzut +/-3*sigma, czyli 6*sigma wskazuje zakres wartości, pomiędzy którymi spodziewamy się napotkać 99,73% wszystkich wyników. Okazuje się jednocześnie, że uogólniony wzór na współczynniki Cp/Pp wyrażony jest nieco inaczej niż wzór (1) i przedstawia się następująco:
$$Cp, Pp = \frac{USL-LSL}{Q_{99,865}-Q_{0,135}}\tag{3}$$
Powyższy wzór należy odczytywać następująco: wartość współczynnika zdolności Cp lub Pp to stosunek przedziału tolerancji do przedziału, w którym oczekujemy 99,73% wszystkich wyników, przy czym w szczególnym przypadku rozkładu normalnego, zakres tego przedziału można wyznaczyć posługując się 6*sigma. Wynika stąd że wzór (1) jest szczególnym przypadkiem wzoru (3) i jest poprawny tylko dla rozkładu normalnego.
Wyjaśnijmy teraz dokładniej sens wyrażeń użytych we wzorze (3). W stosunku do wzoru (1) licznik nie uległ zmianie i dalej przedstawia szerokość przedziału tolerancji. W mianowniku pojawiły się natomiast dwa dziwne składniki. Są to tak zwane kwantyle, które wyznaczają pewną wartość procentową pola pod krzywą rozkładu prawdopodobieństwa. Przykładowo kwantyl 1 (zapisywany jako Q1) wskazuje taką wartość zmiennej losowej (a w naszym przypadku – wartość badanej charakterystyki), poniżej której (ale łącznie z nią) możemy oczekiwać 1% wszystkich wyników, kwantyl 50 (zapisywany jako Q50) wskaże wartość, poniżej której możemy oczekiwać połowy wszystkich wyników. Kwantyl Q50 jest więc jednocześnie medianą. Krótko mówiąc kwantyl o określonym numerze odcina zawsze taką część pola pod krzywą rozkładu, że dla liczby mniejszej lub równej wartości tego kwantyla można spodziewać się wskazanego przez indeks kwantyla procentu wszystkich wyników. Warto tu jeszcze dodać, że jeżeli kwantyle są wyrażone w procentach, często nazywa się je po prostu percentylami.
Przypomnijmy też, że analizując rozrzut procesu mamy na myśli obszar obejmujący 99,73% wszystkich wyników. Oznacza to, że poza tym obszarem znajdzie się 0,27% pozostałych, które symetrycznie musimy rozdzielić pomiędzy lewy i prawy ogon rozkładu. Oznacza to, że z każdej strony pozostanie 0,135% procenta wyników. Graficznie można to wyrazić następująco:
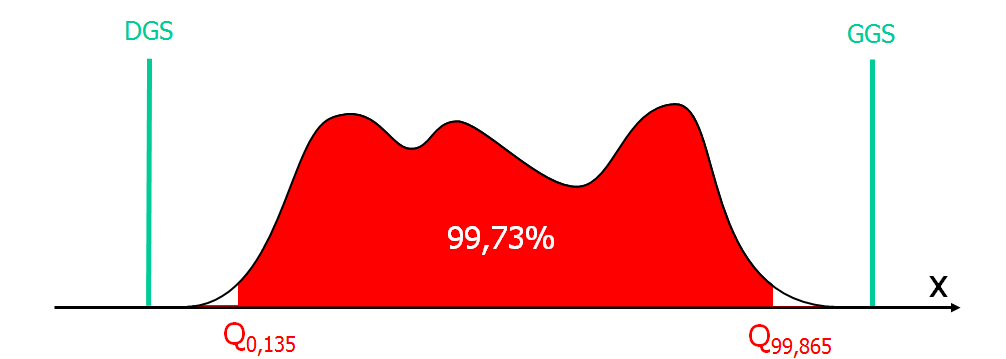
Innymi słowy zapis (Q99,865 – Q0,135) oznacza, że interesuje nas taki procent wyników pod rozpatrywaną krzywą gęstości rozkładu, który obejmuje 99,73% wszystkich wyników.
W tym momencie dochodzimy do kluczowego stwierdzenia. W rozkładzie normalnym przedział 6*sigma jest tożsamy z zakresem 99,73%. Jednak w przypadku innego modelu rozkładu niż normalny 6 odchyleń standardowych wyliczonych z rozpatrywanej próby losowej (pomiarów pobranych z procesu o rozkładzie innym niż normalny) przestaje wyznaczać przedział 99,73%. Konkluzja jest więc następująca – im bardziej rozkład procesu odbiega od normalności, tym większy błąd w ocenie zdolności będziemy popełniać stosując wzór (1). Należy tu też od razu zaznaczyć, że błąd ten może powodować zarówno przeszacowanie zdolności (wtedy będziemy zbyt optymistycznie patrzeć na ryzyka występujące w procesie) jak i jej niedoszacowanie (wówczas będziemy ponosić niepotrzebne nakłady związane z poprawianiem procesu, który tak naprawdę jest dobry).
Analogiczne rozumowanie można przeprowadzić dla współczynników z indeksem k, co powoduje, że wzory dla rozkładów inne niż normalny uzyskują postać:
$$Cp_k, Pp_k = \text{min}\Big\{\frac{USL-{\tilde x}}{Q_{99,865}-{\tilde x}};\frac{{\tilde x}-LSL}{{\tilde x}-Q_{0,135}}\Big\}\tag{4}$$
Warto też zauważyć, że w zmodyfikowanym wzorze zamiast średniej jako miara położenia procesu została użyta mediana. Wynika to z faktu, że w rozkładach innych niż normalny mediana zwykle lepiej wyraża położenie procesu. Warto również dodać, że powyższy wzór można zapisać w postaci:
$$Cp_k, Pp_k = \text{min}\Big\{\frac{USL-Q_{50}}{Q_{99,865}-Q_{50}};\frac{Q_{50}-LSL}{Q_{50}-Q_{0,135}}\Big\}\tag{5}$$
ponieważ mediana jest równoważna kwantylowi 50-temu.
Przykład praktyczny:
Wyjaśnimy teraz na przykładzie, jakie praktyczne znaczenie ma zastosowanie wzorów (1) i (2) lub (3) i (4). Załóżmy, że dokonywany jest pomiar płaskości pewnej powierzchni. Mierzona charakterystyka została zdefiniowana następująco:
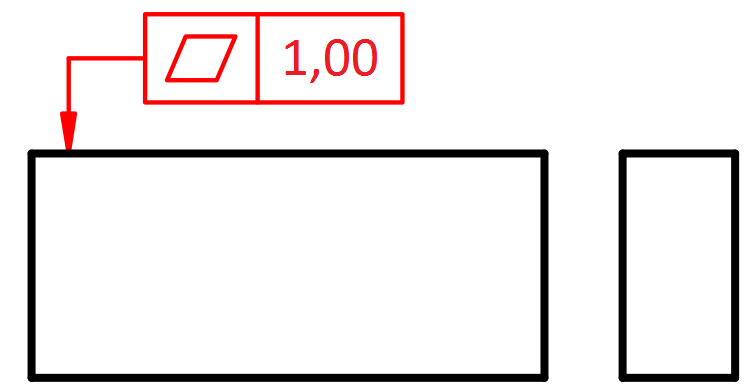
Wykonano pomiar 100 sztuk wyrobów i dla każdego wyznaczono odchyłkę płaskości. Uzyskane wyniki pomiarów obrazuje poniższy histogram (wszystkie zaprezentowane wykresy i obliczenia zostały wykonane w programie Minitab):
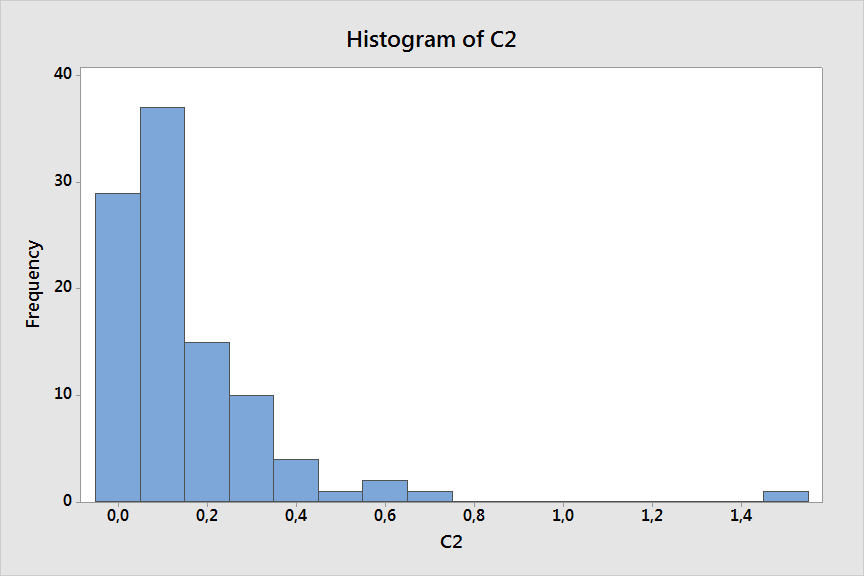
Już z wstępnej analizy wizualnej wynika, że dane te nie odpowiadają krzywej Gaussa. Zwróćmy uwagę, że w uzyskanych danych nie ma wartości ujemnych. Wynika to ze specyfiki rozpatrywanej charakterystyki – odchyłka płaskości jest wyznaczana jako odległość między dwiema płaszczyznami równoległymi, w których zawiera się zaobserwowana powierzchnia. W odniesieniu do przedstawionej wcześniej specyfikacji można to zwizualizować następująco:
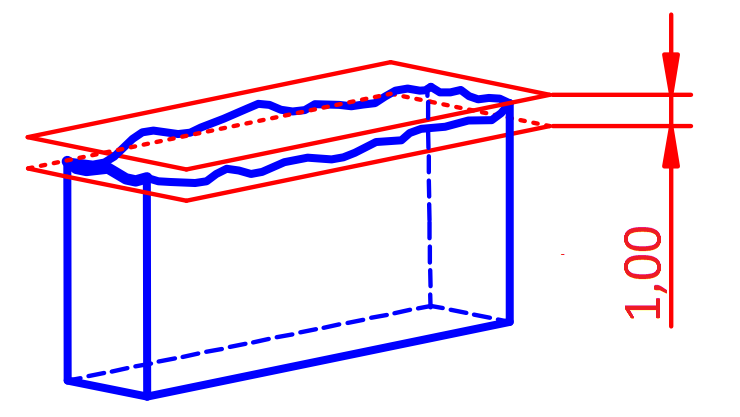
Jest to więc zawsze wartość dodatnia, zaś idealnej płaskości odpowiada wynik 0. (Więcej na temat tolerancji płaskości i innych tolerancji geometrycznych można dowiedzieć się na szkoleniu Tolerowanie i wymiarowanie geometryczne).W takim przypadku możemy stwierdzić, że 0 nie jest dolną granicą specyfikacji (LSL – Lower Specification Limit), ale granicą fizyczną (LB – Lower Boundry).
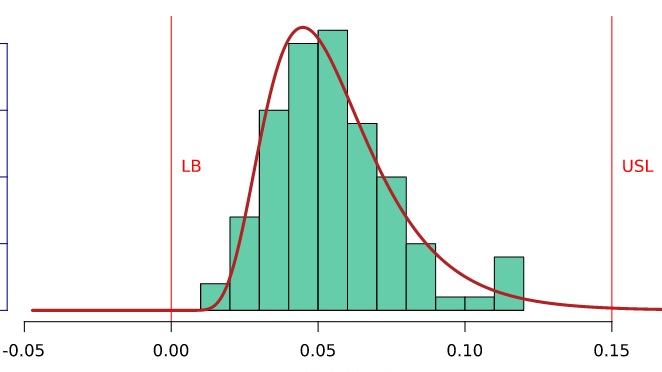
Mimo wyraźnego braku normalności w uzyskanym wykresie histogramu podjęto próbę wyliczenia zdolności dla rozkładu normalnego (a więc z wykorzystaniem wzoru z 6*sigma). Dało to następujący rezultat:
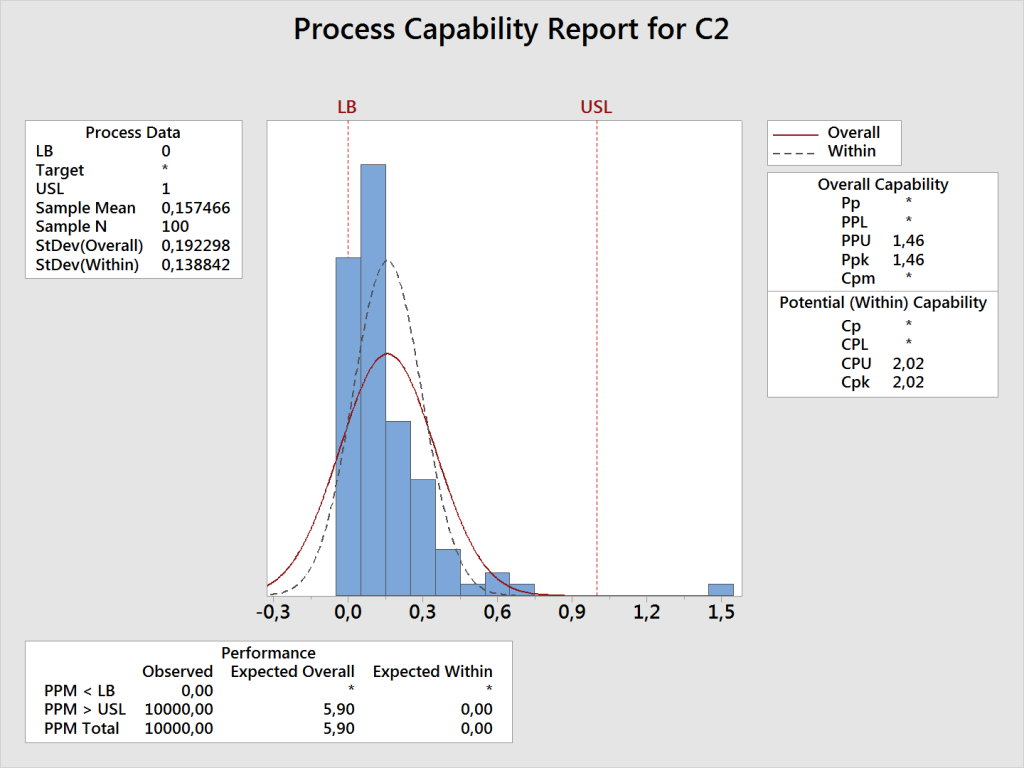
Jak widać na powyższym rysunku, zostały wyznaczone tylko wartości Cpk i Ppk, ponieważ wartość 0 została określona jako granica fizyczna (na wykresie oznaczona symbolem LB), która ze swojej natury jest nieprzekraczalna, a więc nie jest możliwa odchyłka ujemna. Należy tu podkreślić, że sam algorytm wyznaczania zdolności dla rozkładu normalnego zadziała zawsze, niezależnie od słuszności przyjęcia tego modelu – z punktu widzenia metody wyznaczana jest po prostu średnia oraz odchylenie standardowe z zebranych danych, co jest wykonalne bez względu na faktyczny rozkład danych.
Następnie te same dane przeliczono dobierając inny model rozkładu (w tym przykładzie logarytmiczny normalny). Jak widać na poniższym wykresie, teoretyczna krzywa gęstości (czerwona linia) jest znacznie lepiej dopasowana do danych empirycznych pokazanych na histogramie. Jednak co ważniejsze, tym razem w mianowniku wzoru na zdolność nie zastosowano wartości 6*sigma, lecz odpowiednim algorytmem wyznaczono przedział 99,73%.

Jakie wynikają z tego konsekwencje dla decyzji odnośnie zdolności badanego procesu? Przyjmijmy w tym przykładzie, że dla rozpatrywanej charakterystyki klient oczekuje osiągnięcia poziomu zdolności Ppk minimum 1,33. W przypadku, w którym przyjęto założenie o normalności, współczynnik Ppk wyniósł 1,46. Możemy więc przypuszczać, że proces spełnia wymagania zdolnościowe. Jeżeli jednak podczas wyznaczania zdolności zastosujemy rozkład lognormal (który, jak pokazuje wykres, znacznie lepiej pasuje do danych empirycznych), uzyskany współczynnik Ppk wyniesie tylko 0,8, a więc znacznie poniżej wymagań. Znaczenie tej różnicy dobrze obrazuje wartość współczynnika Expected Overall Performance na obu wykresach – oczekiwany poziom niezgodności w przypadku przyjęcia rozkładu normalnego wynosi tylko 6 ppm, jeżeli natomiast zostanie zastosowany model lognormal, wartość ta wzrasta do 8200 ppm, czyli ok. 0,8% wyrobów będzie niezgodnych.
Z powyższego przykładu wyłania się jednoznaczny wniosek – dobór właściwego modelu rozkładu podczas wyznaczania zdolności procesowej może mieć duży wpływ na uzyskany wynik, a tym samym zaniechanie poszukiwań tego modelu może prowadzić do błędnych wniosków na temat stanu procesu.




